Wer versucht die digitale Audio Reproduktion mit dem Verständnis über analoge Audiotechnik zu verstehen, wird wohl kaum um Irrtümer und Trugschlüsse herumkommen. Besonders die Marketingabteilungen der Hersteller scheinen endlos in „digitale“ Fallen und Peinlichkeiten zu treten.

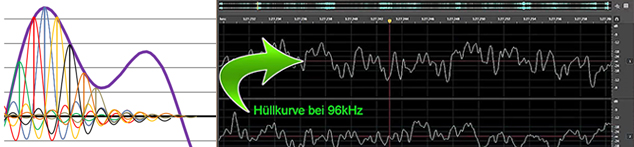
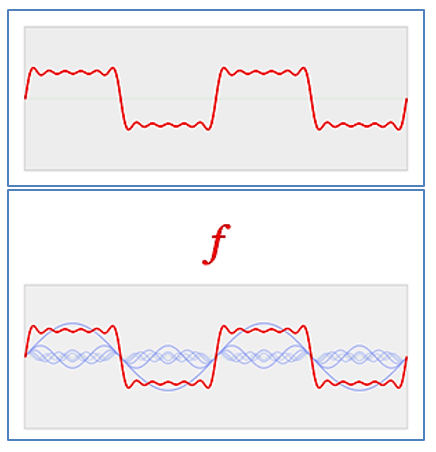
Zwei weit verbreitete Irrtümer sind: a) das zurückgewandelte digitale Signal ist treppenförmig und b) die Information zwischen den Abtastwerten (Samples) ist unwiederbringlich verloren. Für diese Wahrnehmung sind seit der Einführung der CD 1983 herumgereichte Grafiken wie diese verantwortlich:

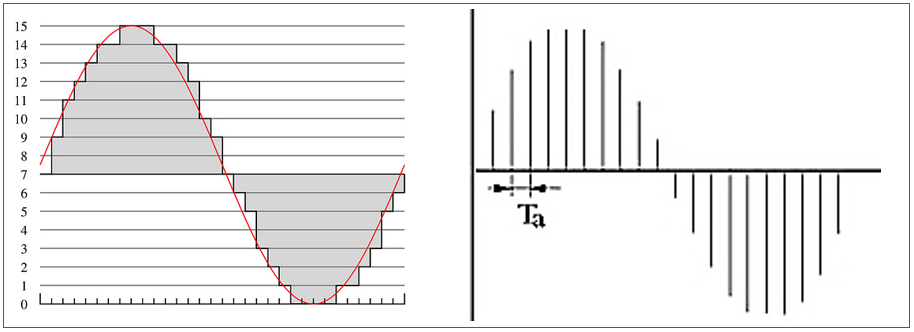
Bilder 1 und 2: Grafiken, die zu Fehlschlüssen verleiten.

Die Grafiken sind nicht falsch, nur die Schlussfolgerungen daraus, denn sie zeigen nicht das rekonstruierte analog Signal, sondern nur Zwischenschritte der digitalen Signalverarbeitung. Mit HD-Audio (High-Res-Audio) hat sich das Feld von Missverständnissen und bewusster oder unbewusster Fehlinformation noch vergrössert. Doch alles der Reihe nach.

Will man die digitale Audio Technik nur einigermassen korrekt erfassen, kommt man nicht darum herum sich mit den Grundelementen der Akustik (Musik), dem menschlichem Hören und technisch mathematischen Aspekten zu befassen. Da dieser Komplex den Umfang eines einzelnen Blog Beitrages bei weitem sprengt, wollen wir heute das Thema in geraffter Form angehen und in weiteren Blogs die einzelnen Aspekte im Detail darstellen. Dies hat die Konsequenz, dass die Aussagen im heutigen Beitrag (noch) nicht für jeden Leser zwingend schlüssig sein können.

Die Ausgangslage 

Musikinstrumente und Stimmen erzeugen Luftdruckschwankungen die vom Ohr oder einem Mikrofon aufgenommen und in elektrische Signale umgewandelt werden. Beim Menschen werden die Druckschwankungen über das Trommelfell in die Hörschnecke (Cochlea) geleitet, wo sie als elektrische Nervenimpulse ins Gehirn gelangen. Die wellenförmigen Luftdruckschwankungen sind in den Rillen einer Vinyl Schallplatte mechanisch gespeichert und somit sichtbar.

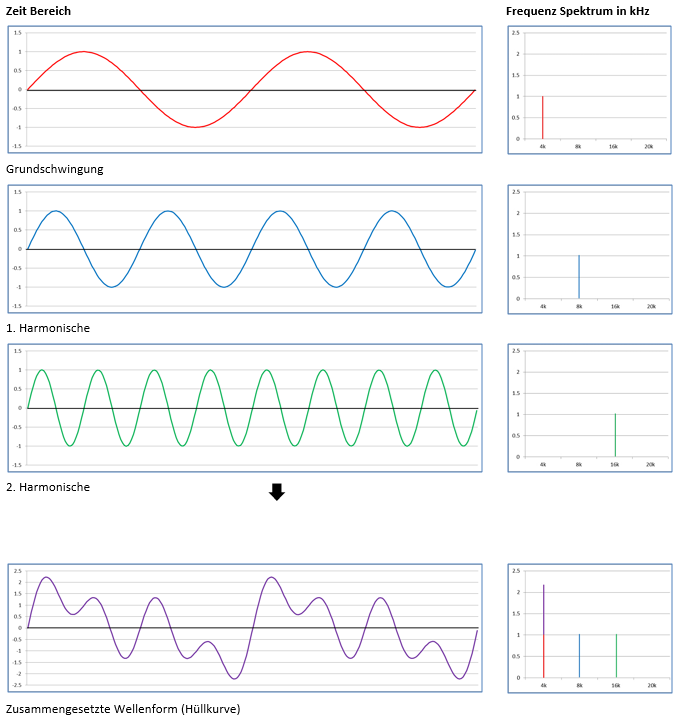
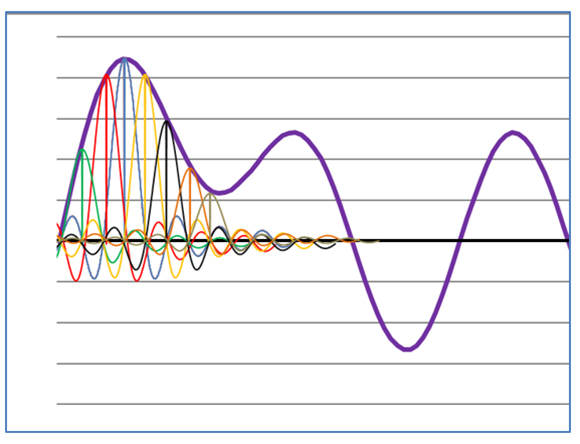
Ein von einem Instrument (Stimme) erzeugter Ton besteht aus sinusförmigen Grund- und Oberschwingungen, die sich als Summe in einer Hüllkurve darstellen und als Klang wahrgenommen wird.

Bild 3: Aus Grund- und Obertönen eines Instrumentes entsteht durch Addition und Subtraktion der einzelnen Schwingungen die Hüllkurve.

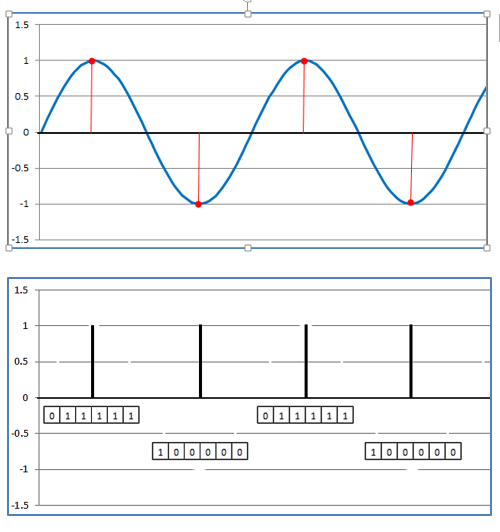
Die violette Hüllkurve zeigt die Druckschwankungen in der Luft (Schallereignis), die wir hören oder analog oder digital speichern wollen. In der analogen Welt werden die Druckschwankungen zeitkontinuierlich als Ausrichtung von magnetischen Partikeln (Tonband) oder mechanische Verformung eines Materials (Wachs, Schellack, Vinyl) gespeichert. Bei der digitalen Speicherung werden die Druckschwankungen, die vom Mikrofon in ein analoges, zeitkontinuierliches elektrisches Signal gewandelt werden, in zeitdiskrete, numerische Werte konvertiert. Zeitdiskret heisst, dass das analoge Signal in zeitlich festgelegten Intervallen abgetastet wird und der Amplitudenwert (Schwingungsweite) als Zahlenwert gespeichert wird. Dies zeigt die Grafik 2, welche allerdings in der dargestellten Form technisch gar nicht existiert, sondern lediglich eine Veranschaulichung des Pulszuges ist. Bei der CD erfolgt die Signalabtastung 44‘100-mal pro Sekunde. Der Amplitudenwert wird mit einer Wortlänge von 16 Bit erfasst.

Grafik/Bild 4 zeigt das Signal im zeitlichen Verlauf und als Frequenzspektrum (Zeitbereich/Frequenzbereich). Diese beiden Aspekte zeigen ein und dasselbe aus zwei verschiedenen Blickwinkeln: wie ist der Kurvenverlauf eines Klanges und aus welchen Sinusfrequenzen setzt er sich zusammen. Dieser Zusammenhang ist wichtig zum Verständnis der digitalen Signalverarbeitung. Die meisten Irrtümer und Missverständnisse zum Thema entstehen, weil dieser zwingende Zusammenhang nicht erkannt wird. Zeit und Frequenz werden als unabhängige Faktoren betrachtet – was falsch ist.

Unsere Hüllkurve liegt nun nicht als mechanische Rille, sondern als eine Reihe von Zahlenwerten vor.

Bild 4: Signalabtastung und Binär-Werte (stark vereinfachte Darstellung)

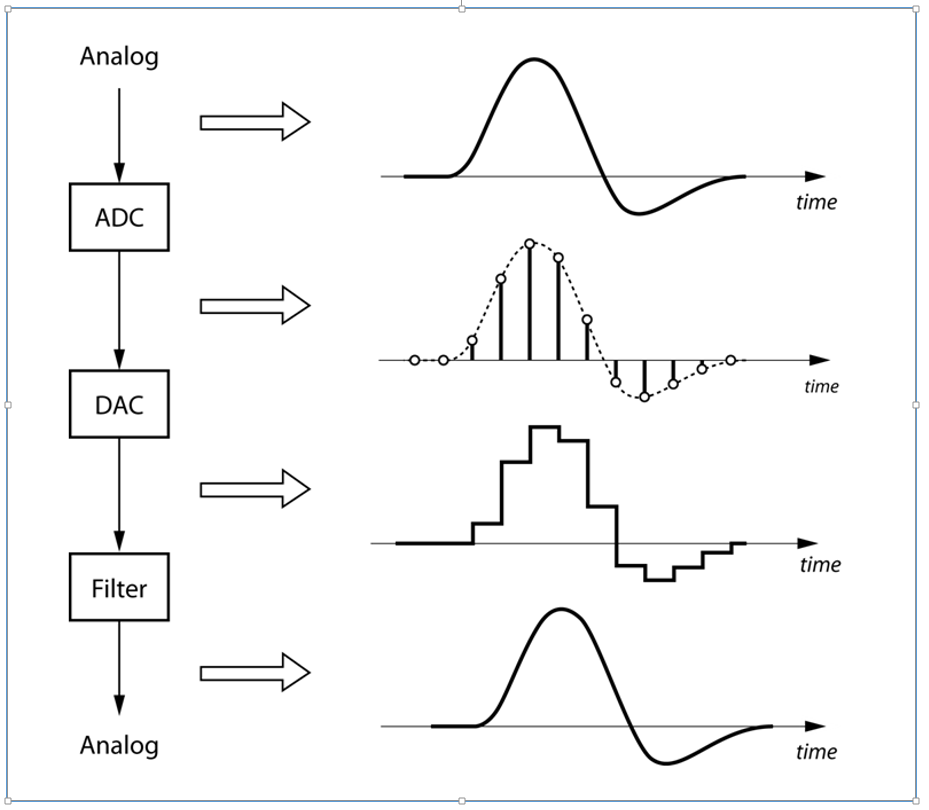
Lässt sich nun aus diesen Zahlen wieder die originale analoge Wellenform herstellen? Ohne Treppen und inklusive der Information zwischen den Abtastwerten (Samples). Die Antwort ist: JA.

Bild 5: Vollständiger A/D-D/A-Zyklus

Warum stimmt diese Aussage? Ganz einfach: das analoge Signal wird aus den Zahlenwerten rekonstruiert (Mathematisch: Multiplikation des Zahlenwertes mit der Sinc-Funktion). Auch die Information zwischen den Samples wird wiederhergestellt. Sie erinnern sich – Geometriestunde: eine Gerade wird mit zwei Punkten definiert und kann mit Hilfe der zwei Punkte auch rekonstruiert werden. Nun kommt der spontane Einwand: Töne bestehen aber nicht aus Geraden. Richtig! Die Rekonstruktion des Tonsignals ist ja auch nicht eine simple Technologie, wie das ziehen einer Line mit dem Lineal. Hier kommt nun der etwas komplizierte, technische Teil, den ich versuche in diesem ersten Blogbeitrag zum Thema stark vereinfacht zu vermitteln.

Bei der Rekonstruktion des analogen Signals wird in einem frühen Schritt die Amplitude als elektrischer Spannungswert aus den Zahlenwerten erzeugt. Dieser Wert wird bis zum nächsten Abtastwert gehalten. Hier kommt nun die Grafik/Bild 1 ins Spiel. Wir sehen diese berühmten und für alle möglichen Aussagen verwendeten Treppenstufen. Eine einzelne Treppenstufe repräsentiert ein Rechtecksignal. Nun eine wichtige Erkenntnis zum Verständnis: Auch ein Rechteck Signal besteht aus lauter Sinusschwingungen. Schauen wir uns ein Rechtecksignal einmal genauer an.

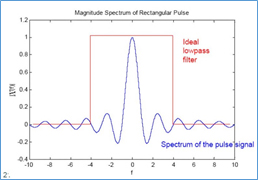
Um ein perfektes Rechteck Signal erzeugen zu können müssen viele Oberschwingungen vorhanden sein. Im Bild/Grafik 7  reicht das Obertonspektrum nicht aus, um ein perfektes Rechteck Signal zu erzeugen, es bleibt eine Restwelligkeit.

Bild 6: Auch ein Rechtecksignal besteht aus lauter Sinusschwingungen

Unsere Treppenstufe ist ebenfalls ein Rechtecksignal und durch Filterung (Bandlimitierung) wird aus der Treppenstufe ein Sinc-Puls:

Bild 7: Sinc-Puls

Aus den einzelnen Rechteckstufen ergeben sich eine Reihe von Sinc-Pulsen. Die Schwingungszüge addieren und subtrahieren sich zur violetten Hüllkurve, die so vollständig rekonstruiert wurde.

Bild 8: Rekonstruktion der Schwingung mit der Sinc-Fukntion

Folgerung: ein Musikstück bei dem nie Signalanteile (Frequenz) höher als beispielsweise 19kHz vorkommen, wird bei einer Samplingfrequenz von 44.1kHz (CD) die genau gleiche Hüllkurve nach der Digital-Analog-Wandlung haben, wie wenn das Signal mit 88.2kHz gesampelt wurde (Basis: moderne Wandlertechnologie). Die mit 88.2kHz verdoppelte Samplingrate ermöglicht die Aufzeichnung einer höheren Grenzfrequenz von maximal 44.1kHz (bei der CD ist bei 22.05kHz Schluss). Da das Signal in unserem Beispiel 19kHz nicht übersteigt, erzeugen beide Systeme das gleiche Resultat. Das Auflösungsvermögen eines digitalen Systems (Frequenz UND Zeitbereich) wird von der maximal übertragbaren Frequenz bestimmt und nicht wie nah die Samples beieinander liegen. Wir werden in einem späteren Blog aufzeigen, wie man Grafiken mit dem Sinc-Puls für irreführende Aussagen umdeuten kann.

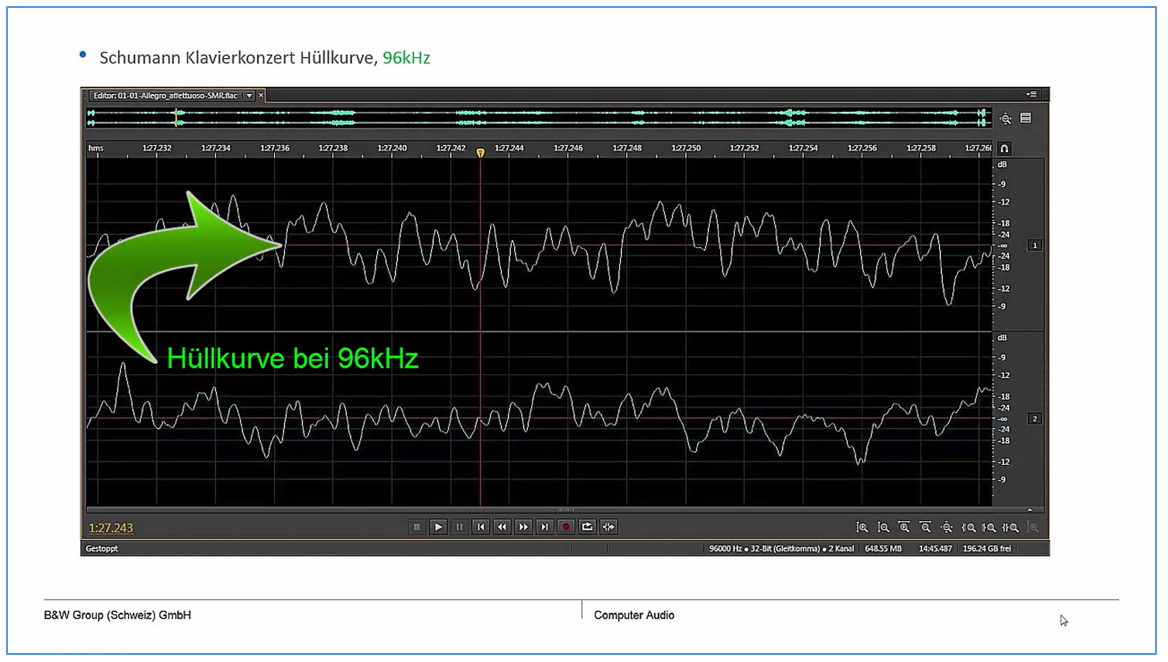
Bild 9: Hüllkurven Vergleich 96/192Khz Samplingfrequenz und MP3 Datenreduziert, auf Bild klicken um Film zu starten

Somit stellt sich die Frage, wie hoch die höchste vorkommende Frequenz (Oberschwingung) eines Instrumentes ist. Dieser Faktor bestimmt die notwendige Samplingrate. Auch zu dieser Frage später mehr.

Und nicht zu vergessen: wie hört der Mensch, welches ist die höchste Frequenz die wir wahrnehmen können? Wie hören wir überhaupt? Hören ist ein kognitiver Prozess, nicht nur die Frage was das Gehör effektiv an Impulsen ans Gehirn weiterleiten kann.

Auch wenn für heute vermutlich noch Fragen offen sind, zentral ist das Wissen, dass es keine Treppen im analogen Signal nach der D/A-Wandlung hat und die Information zwischen den Samples ist vollständig wiederhergestellt.

Wir werden in weiteren Blogbeiträgen das Thema Digital Audiotechnik noch weiter vertiefen, Punkte wie Nyquist Theorem, Wandler Technologien, Signalformate, Jitter, Dynamik, HD-Audio usw. ansprechen und auch die Hörpsychologie miteinbeziehen. Dies alles theoretisch und anhand von konkreten Beispielen thematisieren und wir werden Audio-Mythen auf ihren Sinngehalt prüfen.