Die Formate WAV, FLAC und DSD haben wir im letzten Blog thematisiert. Diese Container Formate, welche das Handling der Musikdateien beeinflussen,  lassen sich mit unterschiedlichen, klangbestimmenden Auflösungen füllen. Da hat sich in den letzten Jahren ein wahres Rennen um immer höhere Wortlängen und Samplingraten etabliert. Je mehr desto besser ist die Devise und je besser desto teurer die Logik der Content Anbieter. Auch die Gerätehersteller wollen mit hohen Zahlenwerten ihre Produkte vom Mitbewerb abgrenzen. Das Ganze funktioniert prima für die Industrie. Auch die Konsumenten lassen sich aus Unkenntnis über die technische und akustische Relevanz immer höherer Samplingraten von diesem Zahlenrennen beeinflussen. Wieso lassen sich so viele Musikliebhaber und Anbieter von Musik und Audiogeräten als Figuren in diese Commedia dell’arte einbinden? Mit etwas Grundwissen über digitale Audiotechnik lassen sich die Komödianten demaskieren.

Archimago’s Musings  – den Dingen auf den Grund gehen

Archimago’s Musings ist ein kanadischer Blog, welcher den Anspruch nach mehr „Objektivität bei audiophilen Themen“ erhebt. Im Blog vom 4. Juni 2016 stellt Archimago die Frage, ob Sampleraten von 176.4 und 192 kHz Sinn machen.  „Is there any value to 176.4 and 192kHz Hi-Res audio files? A practical evaluation…” . In der Folge analysiert er den Frequenzumfang einiger Musiktitel in seiner High-Res Bibliothek und stellt fest, dass kaum einer der analysierten Titel über ein Frequenzspektrum oberhalb von 40kHz verfügt. Somit eine Auflösung von 24Bit/96kHz das ideale Dateiformat darstellt. Der gesamte Frequenz- und Dynamikumfang von Archimagos Musik kann mit diesem Format gespeichert und reproduziert werden. Den Blogbeitrag und die Screenshots der Titel finden Sie hier.

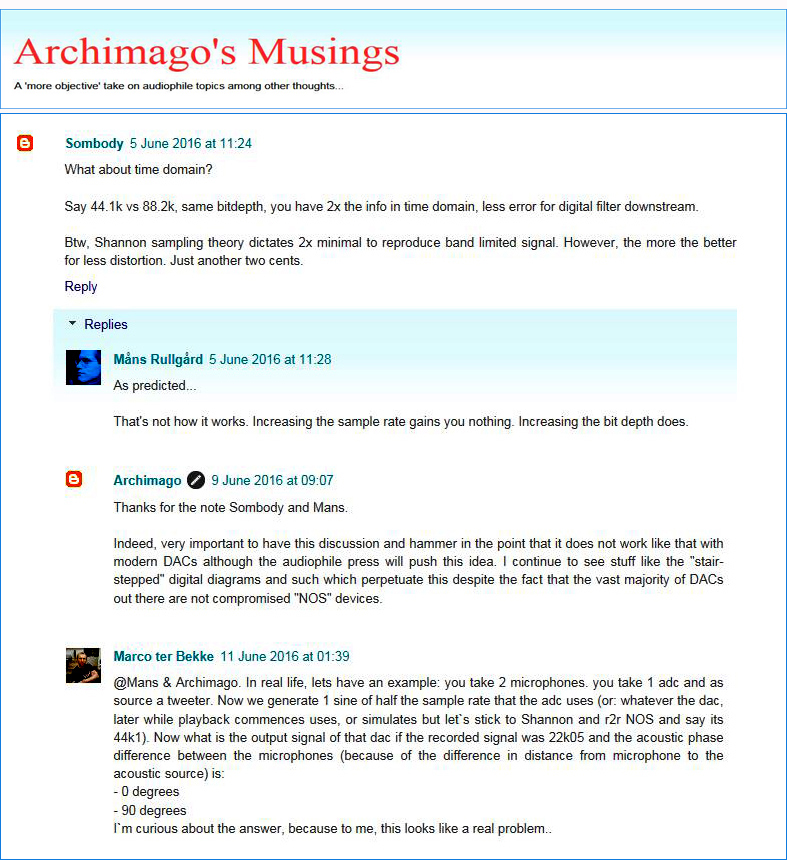
Interessant sind auch die umfangreichen Kommentare auf Archimagos Blog. Da die Themen technisch orientiert abgehandelt werden, sind die Kommentare entsprechend. Auch die Kommentatoren haben teilweise ein fundiertes Musik- und Technikwissen. So schreibt Linux Ingenieur Mans Rullgard als ersten Kommentar zum oben erwähnten Thema:  Für die Unwissenden ist [der Blogbeitrag] das Stichwort für den Kommentar:  „es geht nicht um Frequenzen, es geht um eine verbesserte Auflösung im Zeitbereich „. Aufschlussreich ist ein Kommentar Dialog zwischen Archimago, Mans und zwei weiteren Kommentatoren der den Kern des Themas trifft:

Bild 1: Grösser = auf Bild klicken.

Sombody: „Was ist mit dem Zeitbereich?

Nehmen wir 44.1kHz [Samplingfrequenz] im Vergleich zu 88.2kHz, gleiche Wortlänge, dann haben wir 2x die Information auf der Zeitachse und weniger Fehler beim Digital-Filter. Übrigens, die [Nyquist-] Shannon Abtasttheorie erfordert, dass die Abtastrate doppelt so hoch sein muss wie die höchste im Signal vorkommende Frequenz. Wie auch immer, je mehr desto besser und somit weniger Verzerrungen.“

Mans Rullgard: „Wie vorhergesagt…

So funktioniert es nicht. Die Abtastrate [Samplingfrequenz] zu erhöhen bringt nichts, aber die Erhöhung der Wortbreite [Bit]“

Archimago: Danke für den Kommentar, Sombody und Mans.

In der Tat, es ist wichtig diese Diskussion zu führen und die Sache klar auf den Punkt zu bringen, dass das mit modernen D/A-Wandlern so nicht funktioniert, obwohl die audiophile Fachpresse diese Idee unterstützt. Ich sehe immer wieder diese Grafiken mit den Treppen im digitalen Signalverlauf und ähnliches, die fortwährend gezeigt werden, trotz der Tatsache, dass die überwiegende Mehrheit der D/A Wandler nicht kompromissbehaftete „NOS“ [Non OverSampling] DACs sind“.

Marco ter Bekke: „An Mans & Archimago. Hier ein Beispiel aus dem realen Leben: man nehme zwei Mikrofone, einen Analog-Digital-Wandler und einen Hochtöner. Nun generieren wir eine Sinusschwingung mit der halben Abtastrate des A/D-Wandlers (oder: die Samplingfrequenz die später bei der Wiedergabe verwendet wird, aber bleiben wir bei Shannon [Nyquist-Shannon Abtasttheorem] und R2R NOS [reine 44.1kHz Wandler mit Widerstandsketten] und bestimmen 44.1kHz. Nun, wie sieht das Ausgangssignal am Digital-Analog Wandler aus, wenn das aufgenommene Signal eine Frequenz von 22.05kHz hat und die akustische Phasendifferenz zwischen den beiden Mikrofonen (auf Grund der Distanz zwischen den Mikrofonen und der akustischen Quelle) wie folgt ist:

– 0 Grad
– 90 Grad

Ich bin neugierig auf die Antwort, weil dies für mich ein reales Problem ist“

Fassen wir zusammen und erarbeiten die Antworten

Zusammenfassend und mit Bezug auf Archimagos Blogtext werden folgende Aussagen gemacht:

Archimago und Mans: Der Frequenzumfang der Musik bestimmt die notendige Abtastrate. In den meisten Fällen genügen 48kHz und 96 kHz. Da in der Musik kaum noch oder keine Signalfrequenzen oberhalb von 40kHz vorhanden sind, sind Samplingfrequenzen oberhalb von 96kHz sinnlos. Ist nichts vorhanden, wird auch nichts aufgezeichnet und die Festplatte wird nur mit Null-Information gefüllt. (> Frequenz).

Sombody: Die Verdoppelung der Samplingfrequenz liefert genauere Resultate im Zeitbereich und es entstehen weniger Verzerrungen (Fehler). (> Zeit)

Marco ter Bekke stellt die Frage ob eine Phasenverschiebung von 90 Grad vom System (A/D-D/A-reproduziert werden kann. (> Phase).

Die Grundlage zum Verständnis: Das Abtasttheorem

Alle Fragestellungen lassen sich mit dem Nyquist-Shannon Abtasttheorem und der Funktionsweise von Analog/Digital- und Digital/Analog-Wandlern zweifelsfrei beantworten.

Das Abtasttheorem besagt, dass in einem digitalen System die Abtastfrequenz (Samplingrate) doppelt so hoch wie die höchste im Signal vorkommende Frequenz sein muss, damit aus den zeitdiskreten, digitalen Werten das zeitkontinuierliche analoge Signal wieder exakt rekonstruiert werden kann.

Diese Regel gilt für ein bandbegrenztes Signal. Oder andersrum formuliert: mit 44.1 Samplingfrequenz lassen sich Tonsignale bis 22.05 kHz speichern, mit 96kHz Tonsignale bis 48kHz usw. Bandbegrenzung bedeutet, dass keine Frequenzanteile oberhalb der halben Samplingrate vorhanden sein dürfen, denn diese Frequenzanteile lassen sich nicht mehr richtig rekonstruieren (Aliasing), da weniger als zwei Samples pro Schwingung erzeugt werden. Die Bandbegrenzung wird mit Filtern erreicht. Die richtige Auslegung dieser Filter ist klangentscheidend. Auch die analoge Wiedergabetechnik setzt Filterelemente für ein korrektes Funktionieren ein.

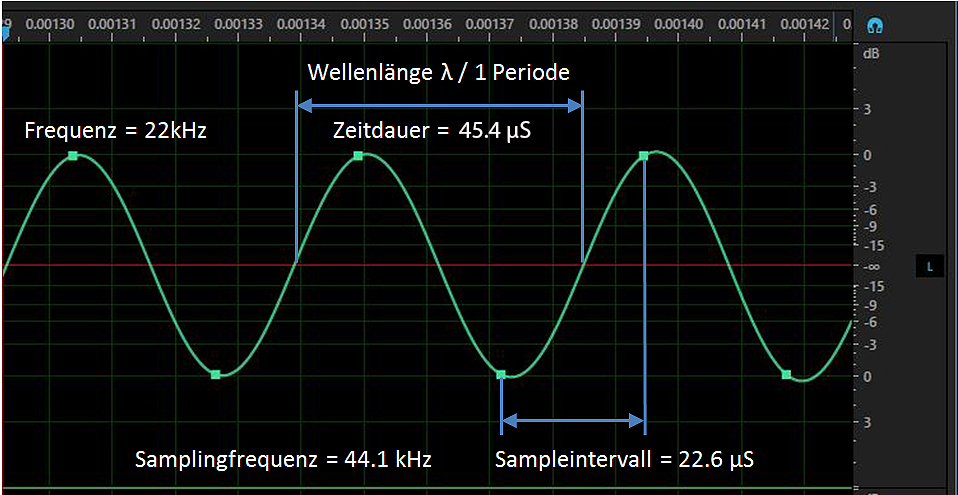
Bild 2: Abtasttheorem: die Abtastfrequenz muss doppelt so hoch sein wie die höchste Signalfrequenz. Dies ergibt bei der höchsten Signalfrequenz nur noch zwei Abtastpunkte. Die Signalfrequenz von 22 kHz ist knapp unterhalb der Systemgrenze von 22.05 kHz für eine Samplingfrequenz von 44.1 kHz. Zwei Abtastpunkte reichen um diese Schwingung exakt rekonstruieren zu können. Man erkennt den leichten Versatz der Samplepunkte, da das Signal 500Hz unterhalb der maximal übertragbaren Frequenz liegt. Bei der Systemgrenze von 22.05 kHz kann nur noch eine Sinusschwingung vorhanden sein, da keine Frequenzanteile oberhalb von 22.05 kHz vorhanden sind. Es passt nur eine Frequenz auf diese zwei Samplepunkte. Grösser = auf Bild klicken.

( > Frequenz). Das Abtasttheorem ist Archimagos Ansatz. Liegt die höchste zu reproduzierende Frequenz des Musiksignals bei rund 40kHz, genügt eine Abtastfrequenz von 96 kHz.

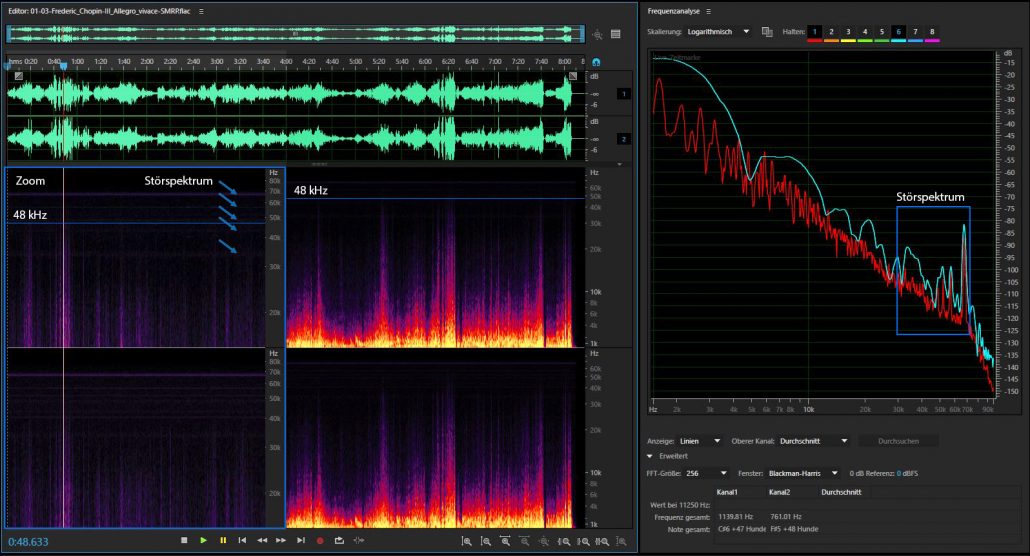
Bild 3: Ergänzend zu den Screenshots auf Archimagos Blogsite hier die Analyse einer 192kHz Datei mit dem 1. Klavierkonzert von Chopin (zufällige Auswahl aus meiner Bibliothek). Auch hier knapp oberhalb von 40 kHz hat es keine Signalanteile der Musik mehr. Die Frequenzanteile oberhalb der menschlichen Hörgrenze von 20kHz bis zu den rund 40kHz sind pegelmässig sehr gering, wie man der FFT Frequenzanalyse im rechten Bildteil entnehmen kann. 24/96 würde für diese Aufnahme nicht nur völlig genügen, vielmehr würden die deutlichen Störfrequenzen – vor allem die bei 68kHz – nicht ins Wiedergabesystem gelangen. Was das genau für Störfrequenzen sind ist nicht klar: vermutlich IM-Verzerrungen. Grösser = auf Bild klicken

Wird eine Frequenz von 20kHz mit 96kHz abgetastet ist das rekonstruierte analoge Signal nicht genauer als bei einer Samplingfrequenz von 44.1kHz, da auch die Information zwischen den Samples vollständig rekonstruiert wird (Link: Digital Basics: – vergessen Sie Treppen und Löcher zwischen den Samples). Ein 96kHz System kann zusätzlich den Frequenzbereich zwischen 22.05kHz und 48kHz aufzeichnen. Ein 192kHz System im Vergleich zu einem 96kHz System die Frequenzen zwischen 48kHz und 96kHz. Ist oberhalb von 48kHz nichts mehr vorhanden, kann das Aufzeichnungsystem auch nichts speichern. Somit wird klar, dass Archimagos Ansatz richtig ist.

( > Zeit). Nun kommt Sombodys Argument ins Spiel, der meint dass eine verdoppelte Samplingfrequenz von z.B. 192kHz mehr Informationen generiere, da ja die Information zwischen den Samples nicht abgetastet wird. Liegen die Samples näher beieinander, desto genauer würden die Kurven bei der D/A-Wandlung wiederhergestellt. Der grosse Irrtum dem viele unterliegen ist, dass sie das Nyquist-Shannon Theorem ausser Acht lassen und den Frequenz- und Zeitbereich als zwei unterschiedliche Aspekte verstehen. Frequenz und Zeit sind dasselbe nur aus unterschiedlichen Blickwinkeln betrachtet. Das Impulsverhalten (oder das zeitliche Verhalten) wird durch die höchste im Signal vorkommende Frequenz bestimmt und steht somit in Bezug zur Bandbreite des Audiosystems. Somebody hat den Zusammenhang zwischen Frequenz und Zeit nicht beachtet und ist daher dem weit verbreiteten Trugschluss „mehr ist besser“  aufgesessen. Bei einem Musiksignal mit einem Frequenzumfang bis 22kHz gibt‘s somit keine Ereignisse (Impulse), die eine kürzere Zeitdauer (Periodendauer) als 45.2 μS haben. Auch der Abtastzeitpunkt hat keinen Einfluss darauf, ob das Signal exakt rekonstruiert werden kann.

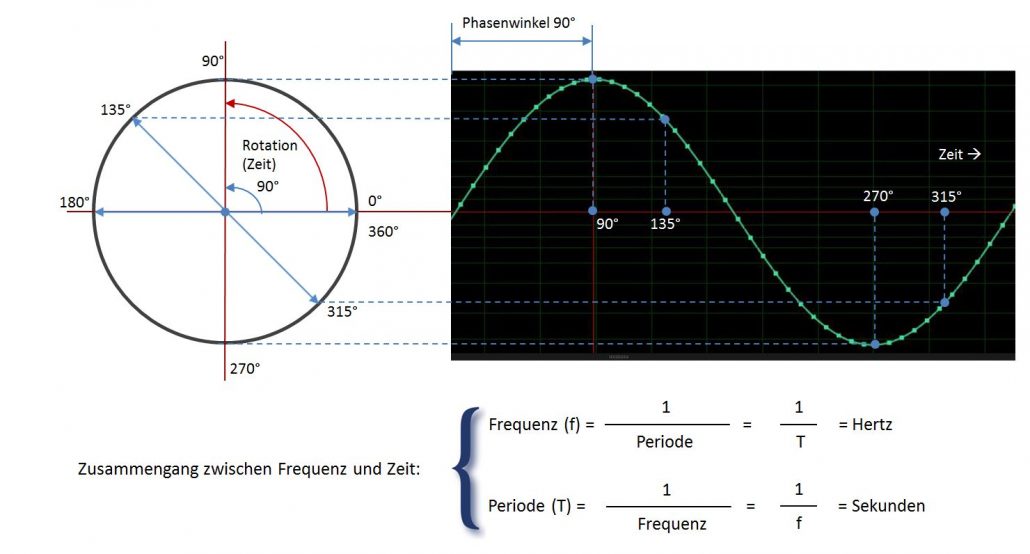
Bild 4: Periode = Zeitdauer eines Schwingungszuges von 360 Grad ist von dessen Frequenz abhängig. Grösser = auf Bild klicken

(> Phase). Marco ter Bekkes Bedenken gehen in die genau gleiche Richtung wie die von Sombody (Informationsverlust zwischen den Samples), da er zweifelt dass eine Phasenverschiebung von 90 Grad vom digitalen System richtig reproduziert werden kann. Eine Phasenverschiebung ist ebenfalls ein Zeitaspekt und kann problemlos reproduziert werden, denn wie erwähnt der Abtastzeitpunkt spielt keine Rolle.

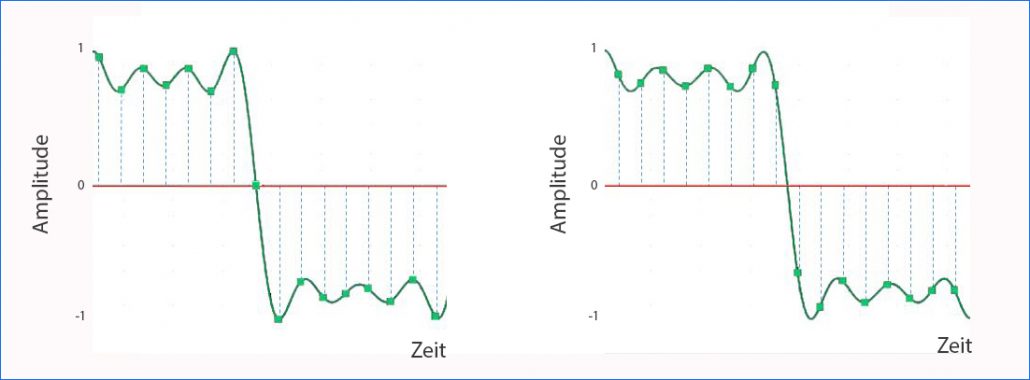
Bild 5: Für die genaue Rekonstruktion der Schwingung spielt es keine Rolle, zu welchem Zeitpunkt innerhalb einer Periode die Schwingung abgetastet wird. Die Abtastung muss nicht genau beim Nulldurchgang oder dem Spitzenwert einer Schwingung erfolgen. Die Richtigkeit bestätigt das Nyquist-Shannon Abtasttheorem. Grösser = auf Bild klicken.

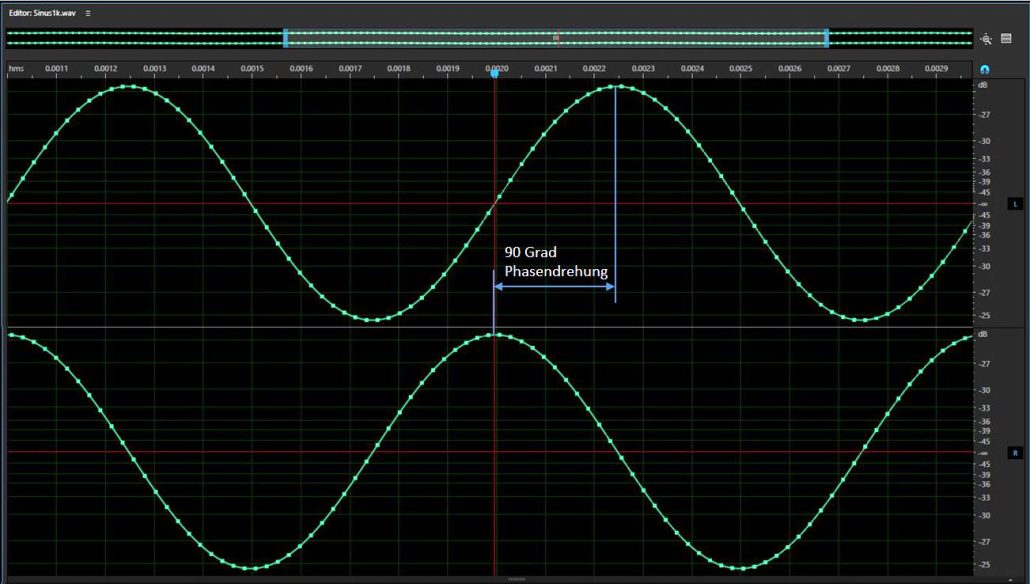
Bild 6: Eine 90 Grad Phasenverschiebung ist kein Problem. Weder bei 1 kHz, wie im Bild oben, noch bei 20 kHz. Grösser = auf Bild klicken.

Ja aber das menschliche Auflösungsvermögen im Zeitbereich!

Bleibt das Faktum, dass das menschliche Auflösungsvermögen im Bereich von 4 μS liegt. Also doch eine Samplingfrequenz von 384kHz? Nein! Denn wir haben gesehen, zu welchem Zeitpunkt ein Signal abgetastet wird ist irrelevant. Eine Phasenverschiebung von x oder y Grad oder von 4 μS wird vom System erfasst und genauso reproduziert. Messungen haben ergeben, dass eine zeitliche Verschiebung eines Signals von 45 Nano-Sekunden in einem mit 44.1 kHz arbeitenden System reproduziert werden kann. Was um den Faktor 100 besser als das menschliche Auflösungsvermögen ist.

Alles nur Theorie?

Was ist mit den Leuten die wortreich klangliche Unterschiede hören und erzählen, wo objektiv nichts vorhanden ist? Hören ist nicht nur eine physikalische Angelegenheit, sondern ein kognitiver Prozess. Unser Hirn produziert aus den elektrischen Sinnesreizen ein Abbild der physikalischen Umwelt. Und da kann uns unser Hirn manchmal ein X für ein U vorgaukeln. Im optischen Bereich sind die Beispiele von Sinnestäuschungen hinlänglich bekannt. Auch im Audiobereich kann die Wahrnehmung durch Selbst- oder Fremdeinwirkung beeinflusst werden. Man ist doch nicht blöd, bezahlt viel mehr für ein 192kHz File um dann den suggerierten Klangvorteil nicht zu hören. Oftmals fehlen auch einfach die Vergleichsmöglichkeiten und man vertraut auf die herumgereichten Mythen und Anekdoten.